Making Convolutional Networks Shift-Invariant Again는 ICML 2019에 소개된 논문으로 약간은 신호처리적인 관점에서 CNN을 다룬 논문입니다. aliasing과 shift-invariant에 대해서 소개하고 있습니다. 이번에는 세세히 리뷰보다는 얻어가야 할 아이디어와 중요한 background위주로 서술해보겠습니다. 다만, 저는 신호처리에 대한 깊은 이해를 가지고 있지는 못하기에 부족한 부분이나 잘못된 부분이 있을 수 있습니다.(피드백은 언제든지 환영! )또한, 논문에 대한 저자의 발표의 흐름과 유사하게 서술할 예정이니 필요하다면 영상 또한 참고하셔도 좋을 것 같습니다.
1. Abstract
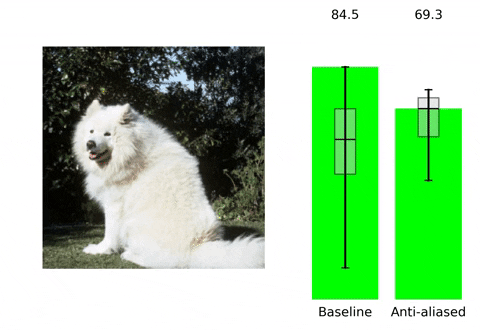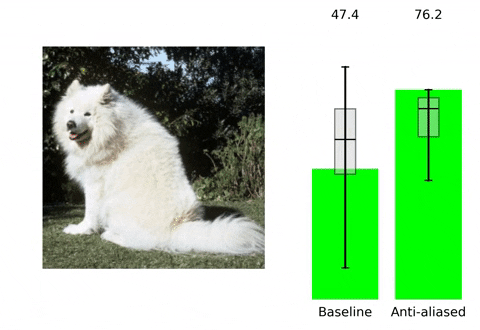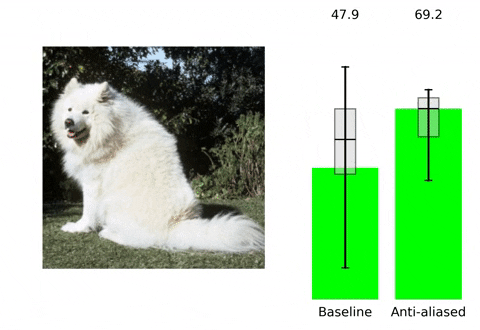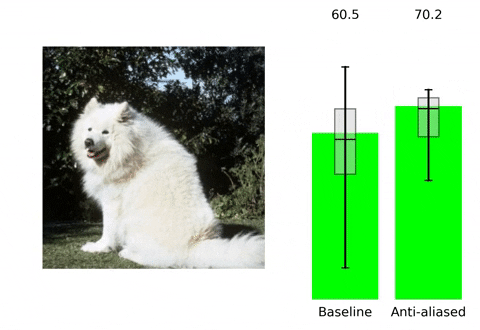
| We show that classic antialiasing applied to modern deep networks can stabilize outputs and improve accuracy. Try a pretrained antialiased network as a backbone for your application. |
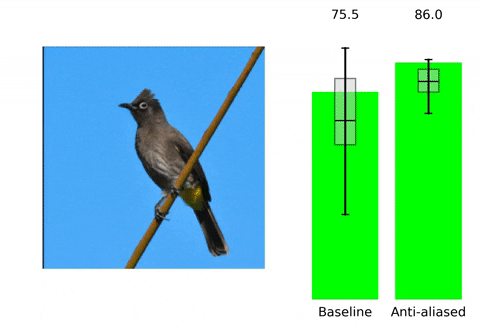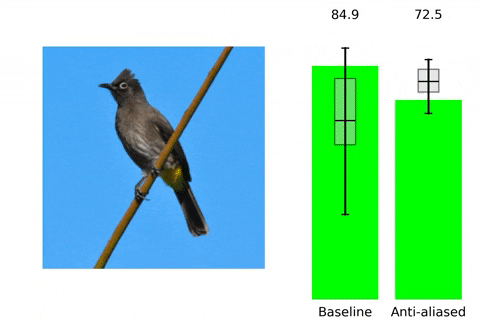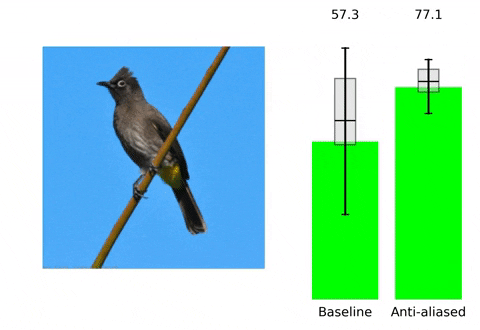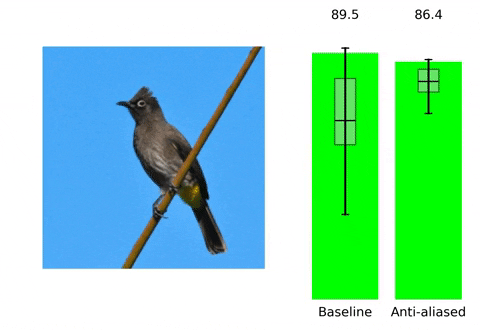
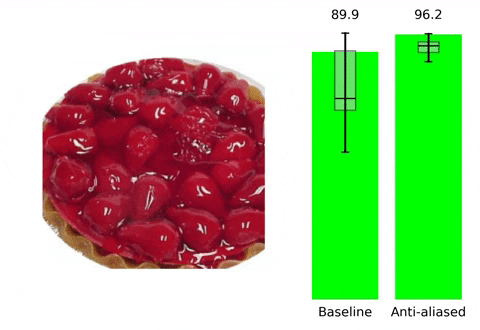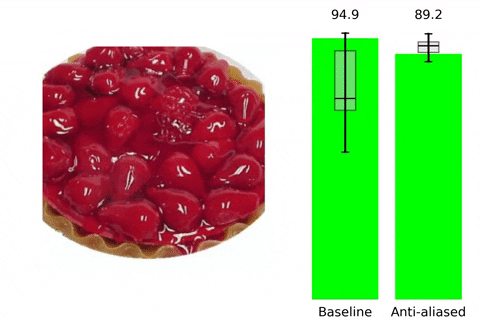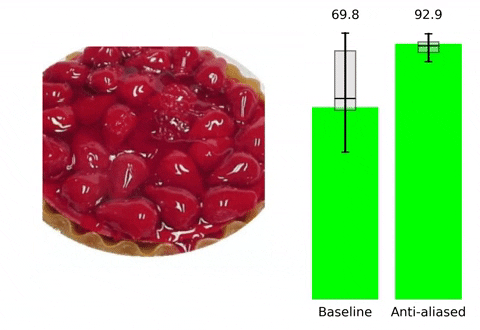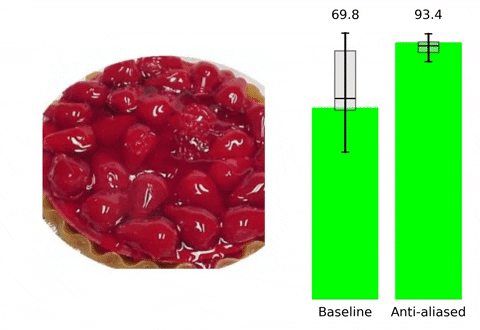
위 contents는 본 논문의 프로젝트 페이지에 소개되어 있습니다. 말하고자 하는 바 또한 다음과 같습니다. 현재 사용되는 Convolutional Neural Network들은 shift-invariant하지 못합니다. 즉, input image에서의 아주 작은 변화( shift x,y등)만으로도 CNN의 output에 큰 변화가 생깁니다. Augmentation 기법이나 다른 연구들을 통해 이러한 문제를 해결하고 더 robust한 모델을 만들기 위해 노력하고 있지만, 저자들은 이러한 문제가 발생하는 이유를 CNN에서 사용되는 max-pooling, strided-convoluton 등의 stride기반의 downsampling methods들이 sampling theorem을 무시하기에 발생하는 일이라고 지적하면서 새로운 해결 방향성을 제시합니다. 실제로 이러한 문제는 위 gif에서 볼 수 있듯이 seemingly inocuous shift와 같은 사람이 인지하기에는 같은 identity를 가진 무해한 변화에도 CNN의 성능에 급격한 차이가 발생하는 것을 통해 확인할 수 있습니다.
2. Background
이러한 내용들을 살펴보기 위해서 신호처리의 기초적인 내용들 중 일부를 살펴보고 가겠습니다. 우선 간단히 신호처리 도메인의 목표와 Nyquist Sampling Theorem 그리고 Aliasing 등에 대해서 간단히 이해해보도록 하겠습니다.
Goal of Signal Processing
Signal Processing의 목표는 간단합니다. Continuous Signal을 받아서 컴퓨터등 디지털 형식으로 처리를 하고 싶은 것입니다. 예를 들어보면 다음과 같은 continuous signal을 받아 이를 컴퓨터에 저장하고 싶다면 어떻게 해야 할까요? 컴퓨터를 아는 사람이라면 이렇게 continuous하게 저장할 수 없다는 것을 알 것입니다. 물론 해당 함수에 대한 수식을 안다면 수식의 coefficient를 저장하면 되지만, 일반적으로 자연계의 signal을 받는다면 수식을 알 수 없을 것입니다.
따라서 공학적 입장에서는 다음과 같은 continuous함수를 샘플링을 통해 discrete signal로 바꿔 저장하게 됩니다. 즉, 동일한 간격으로 정보를 샘플링한 뒤에 샘플링한 정보들을 저장하는 것입니다.
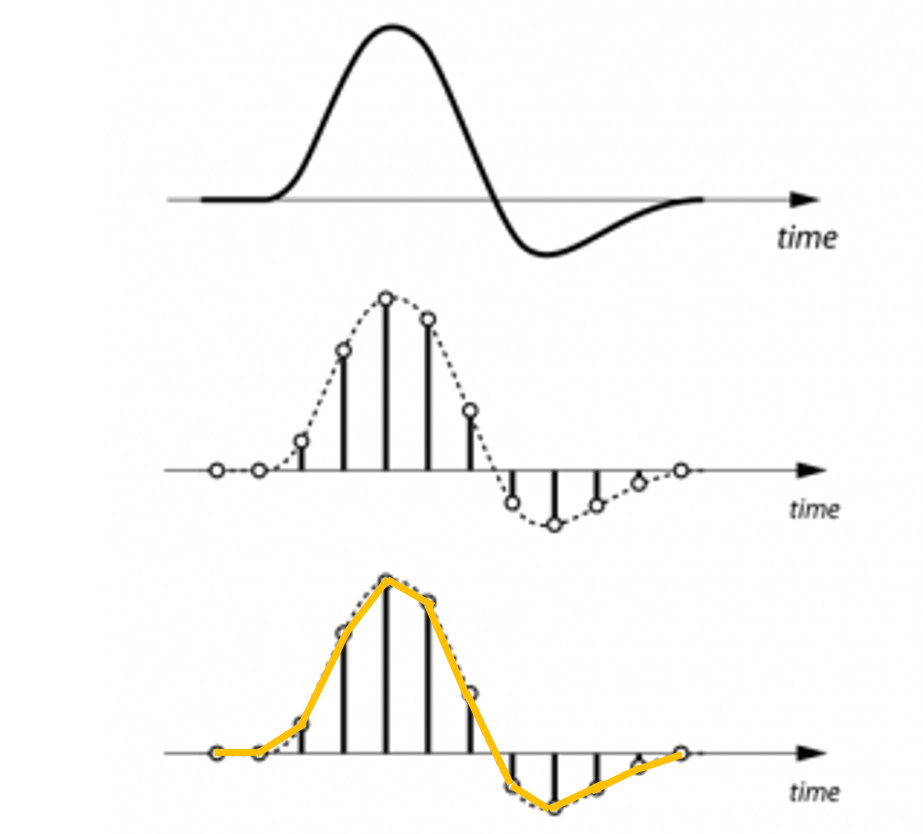
이 때 신호처리의 큰 목표 중 signal reconstruction 즉 신호 복원을 생각해보면 저러한 continuous signal을 컴퓨터에서는 discrete signal로 받았습니다. 하지만, 정말로 원하는 정보는 continuous signal일 것입니다. 따라서 컴퓨터에서는 받은 discrete signal을 constinuous signal로 복원하기를 원합니다.
Aliasing
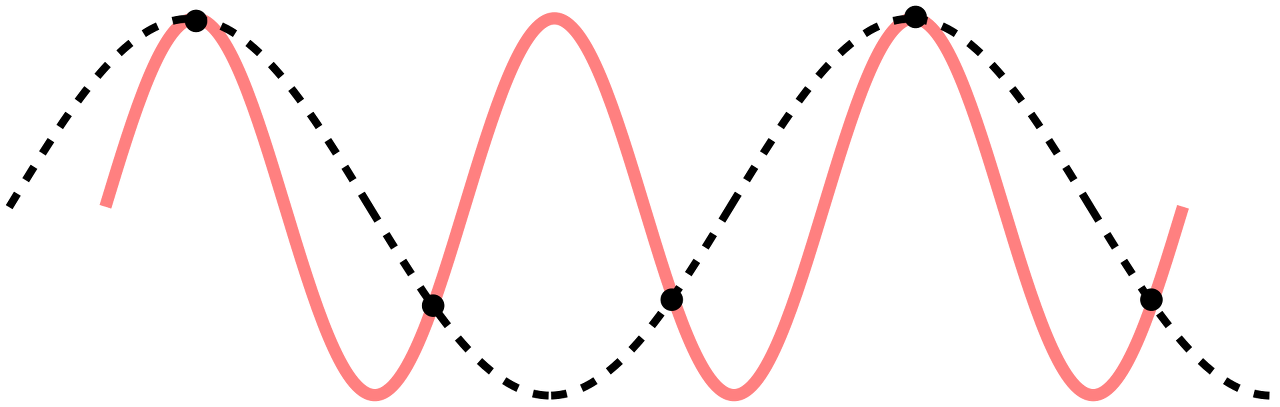
이 떄 충분히 높은 sampling rate ( 샘플링 비율 : 주기별 샘플링 횟수)로 샘플링하지 않았다면 기존 continuous signal의 정보를 온전히 보전하지 못할 것입니다. 즉 다음 이미지에서와 같은 붉은색의 신호를 처리하고자 할 때 검은색 점들처럼 샘플링을 하게 된다면 기존의 신호의 정보가 온전히 복구되지 못하고 샘플링에 의해 얻은 discrete signal의 정보와 실제 continuous signal의 정보는 많이 다를 것입니다. 이렇게 정보가 sampling rate의 부족으로 인해 오로지 전달되지 못하는 것을 혹은 signal의 형태에 왜곡이 생기는 것을 alisaing이라고 합니다.
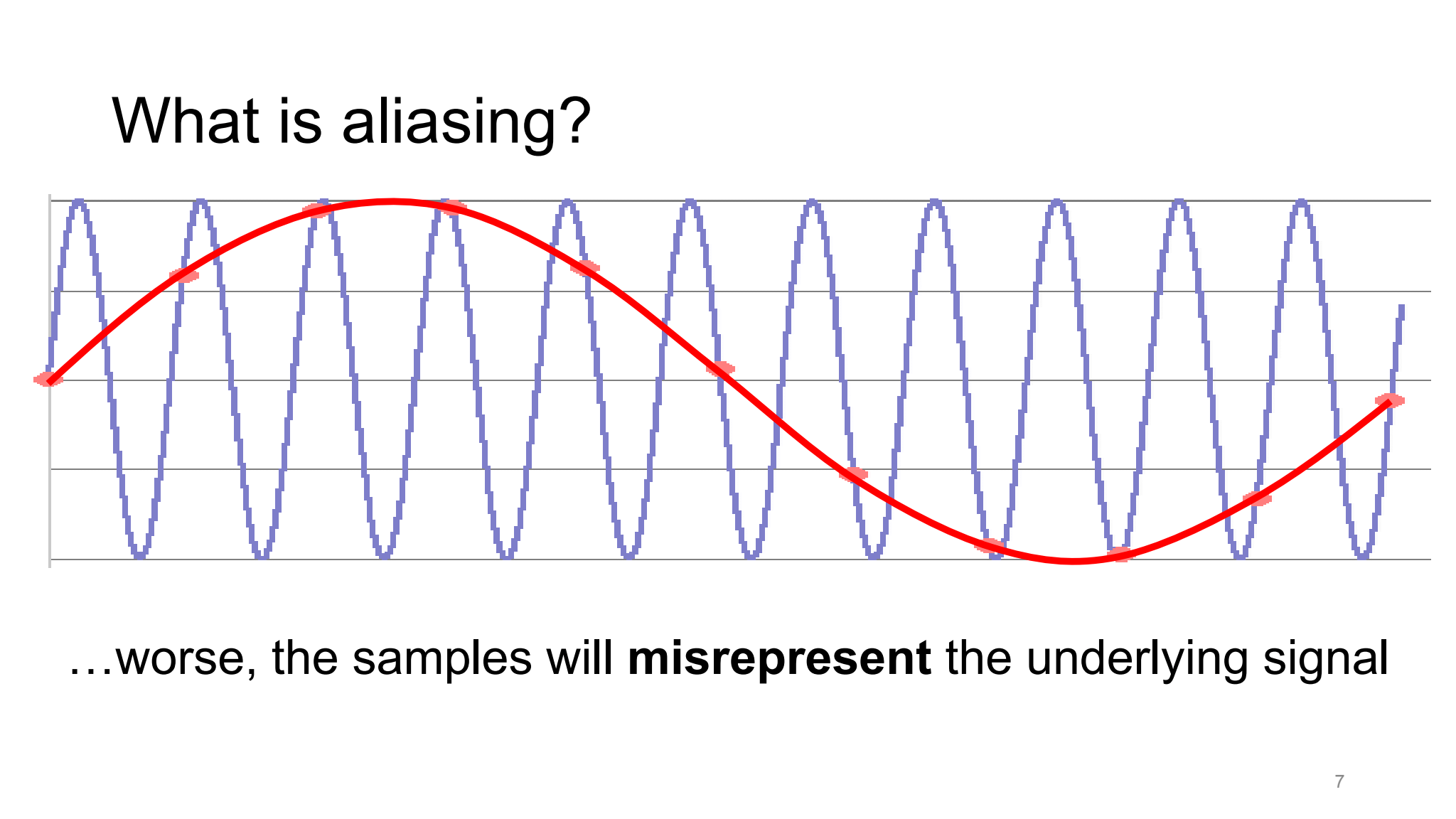
즉, continuous한 정보의 개념을 discrete 한 정보로 처리하기 위해서 제한적인 비율로 sampling 하다 보니 발생하는 일그러짐(신호 왜곡) 현상입니다. 주로 계단현상이라고도 많이 부르는데 이는 주로 다음과 같은 계단 모양으로 왜곡이 발생하기 때문에 그렇습니다.

특히 aliasing 현상은 컴퓨터 그래픽상에서 많이 발생하는데 이 또한 같은 원리입니다. 컴퓨터 그래픽상에서 보여지는 정보가 맨 왼쪽처럼 왜곡이 많이 발생하고 있다면 ( 컴퓨터는 제한적인 resource를 가지기에 sampling rate가 제한적인 것은 당연합니다. ) 이를 보는 사용자 입장에서 매우 불편할 것입니다. 따라서 컴퓨터 그래픽스에서는 이러한 aliasing을 해결하는 anti-aliasing 또한 굉장히 중요한 연구 중에 하나입니다.

Nyquist Sampling Theorem
그렇다면 이러한 alisaing이 발생하지 않기 위해서는 어떻게 해야할까요? 앞서 언급했듯 이는 제한적인 sampling rate로 인해 발생하게 됩니다. 따라서 간단한 방법은 sampling rate를 늘리는 것입니다. 그렇다면 과연 어디까지 sampling rate를 늘려야 할까요?
이렇게 continuous signal로부터 샘플링을 할 때 이렇게 샘플링된 신호를 이용해서 다시 원 continuous signal을 복원할 수 있을 최소한의 sampling rate를 Nyquist rate라고 합니다. 또한 이러한 샘플링 이론을 Nyquist-Shanon Sampling Theorem이라고 합니다. 정리하자면 Nyquist-Shanon Sampling Theorem은 Samplig frequency가 근본적인 신호의 frequency의 2배보다 작다면, 샘플링된 샘플들은 원 시그널을 faithfully represent하지 못한다는 것입니다.
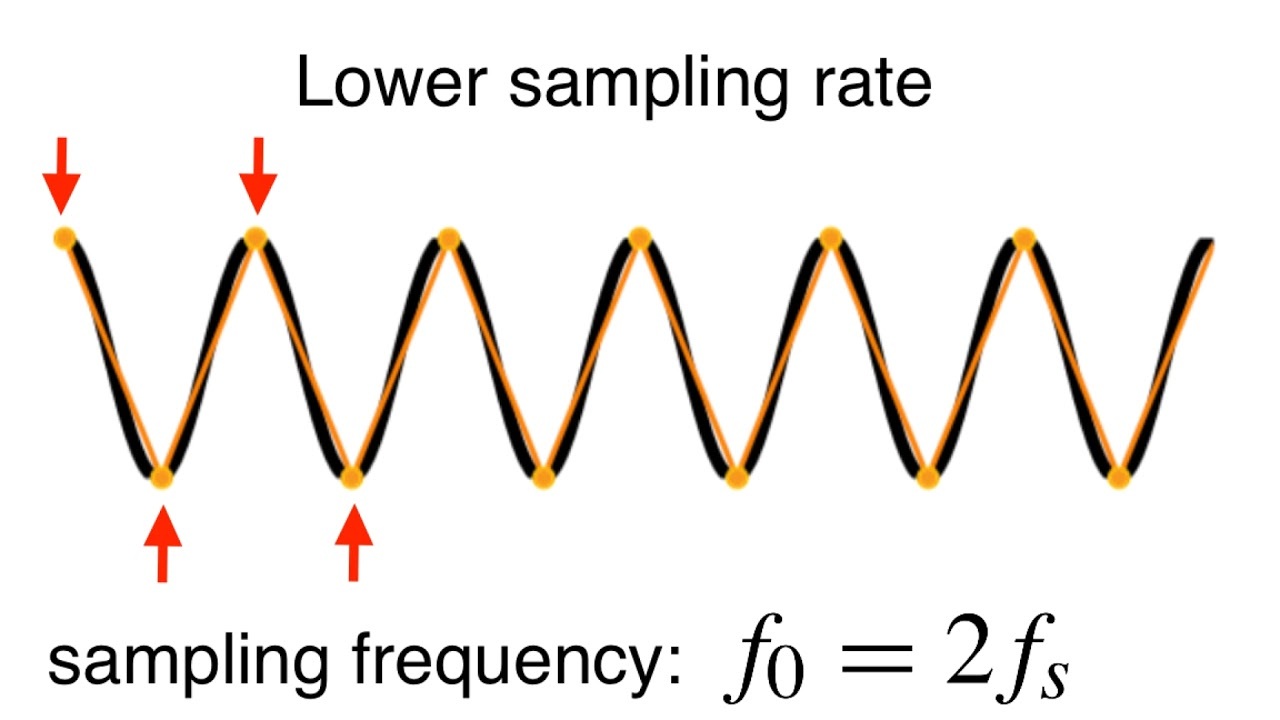
Nyquist Frequency는 입력 신호의 최고 주파수의 2배를 의미하는 것으로 이러한 sampling theorom을 만족시키기 위해서는 이러한 Nyquist rate이상의 sampling rate로 샘플링을 해야 한다는 것입니다.
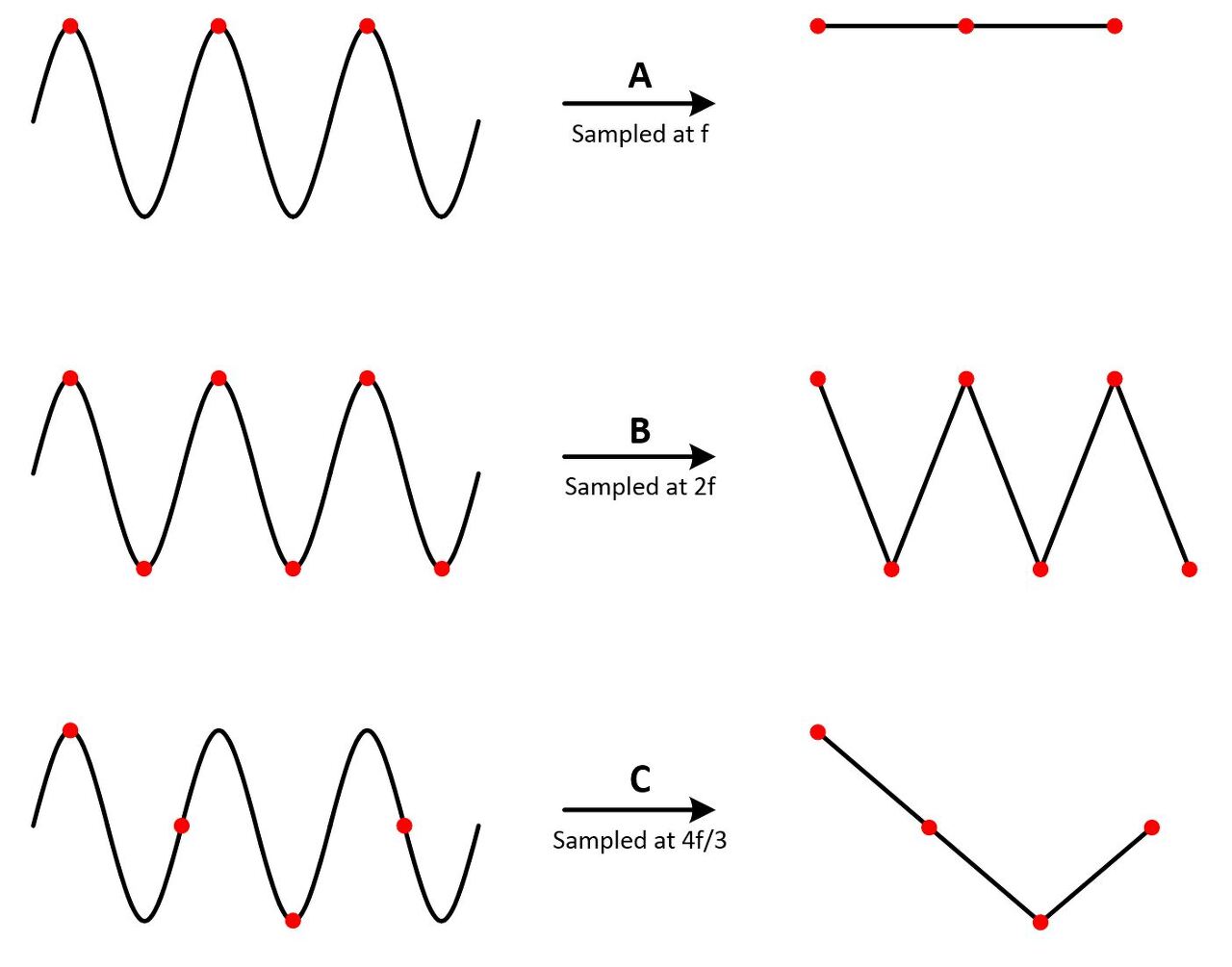
Aliasing ( More Frequency Domain )
이러한 alisaing을 조금 더 주파수 도메인에서 이해해봅시다. 이러한 sampled function의 푸리에 변환식을 적용해보면 다음과 같이 나오게 됩니다.
이때 간단히 푸리에 변환에 대해서 이야기하자면 푸리에 변환(Fourier Transform; FT)은 임의의 입력 함수(주기, 비주기 상관없음)를 받아서 다양한 주파수를 갖는 주기함수(sin, cos)들의 합으로 분해하여 표현하는 것을 말합니다. 신호처리에서의 중요한 맥락인데 어떠한 입력이든 주기함수들의 합으로 항상 분해할 수 있다는 것입니다.
https://supermemi.tistory.com/97
이는 주파수가 F인 신호의 정보를 의미하는 것으로 u 축의 경우 이때 충분한 sampling rate가 보장되지 않는다면 (under-sampling) 다음과 같이 변환된 삼각형모양들의 간격이 좁아지면서 겹치는 부분이 생기는 문제가 발생합니다. 즉, aliasing이 생기는 이유를 푸리에 변환을 거쳐 나온 주기함수들로 설명한다면 다음과 같이 겹치는 부분이 생기기 때문에 signal을 잡아먹어 버려 aliasing이 발생한다는 것이다. ( 신호가 이러한 주기 함수들로 이루어져있다는 것이므로)
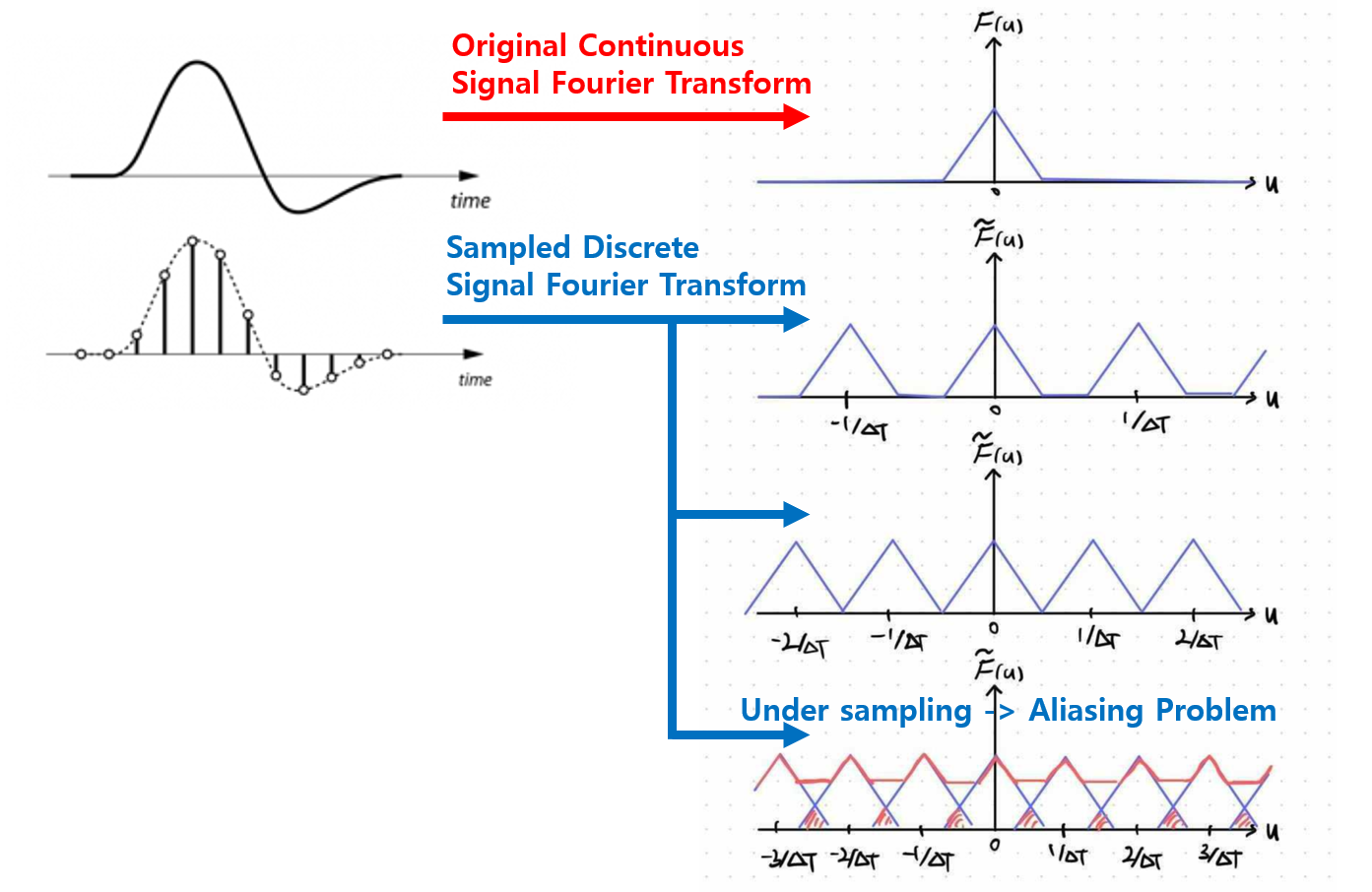
Anti-Aliasing
따라서 맨 아래 그림과 같이 aliasing이 발생하게 되는 것을 막기 위해서는 앞서 이야기했듯 sampling rate를 높이는 것이 방법일 수 있습니다. 하지만, 현실에서는 resource 문제 등등의 이유로 이것이 어렵습니다. 따라서 이를 해결하기 위해서는 보통 anti-aliasing을 해주게 됩니다. 이 때 주로 사용하는 anti-aliasing 방법 중 하나가 low pass filtering 즉 blurring입니다. ( 학부에서 들을 수 있는 신호처리나 그래픽스, 이미지 처리 수업들에서 나오는 blurring을 downsampling에 앞서 사용하는 이유가 이런 맥락에서 입니다. )
이는 말 그대로 신호에서 low frequency부분만 통과시키는 것으로 신호에서 high frequency를 가진 진동하는 부분이나 노이즈로 outlier처럼 튀는 부분을 없애 신호를 더 매끄럽게 smoothing하는 방법입니다.
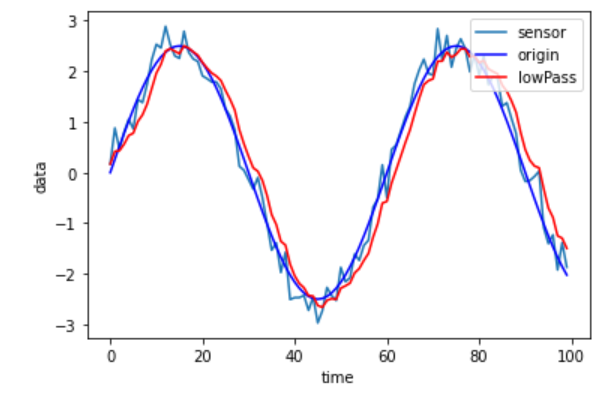
즉 이렇게 low pass filter를 거쳐서 신호를 더 smooth하게 만든다면 sampling이전의 신호에서 aliasing을 발생시키는 부분들을 없앨 수 있는 것입니다. ( 전체적으로 sampling rate가 적어져도 원 continuous signal을 복원하기 쉽도록 smoothing하는 것 - sampling한다고 생각해봤을 때 어떤 그래프가 더 적은 sampling rate로도 원 그래프에 가까워질 수 있을지 간단히 생각해보면 좋겠습니다.)
이를 위에서 봤듯이 푸리에 변환식을 적용한 것에 대해서 생각해보자면 다음과 같이 고주파수 부분을 그냥 잘라내는 것으로 생각할 수 있습니다.
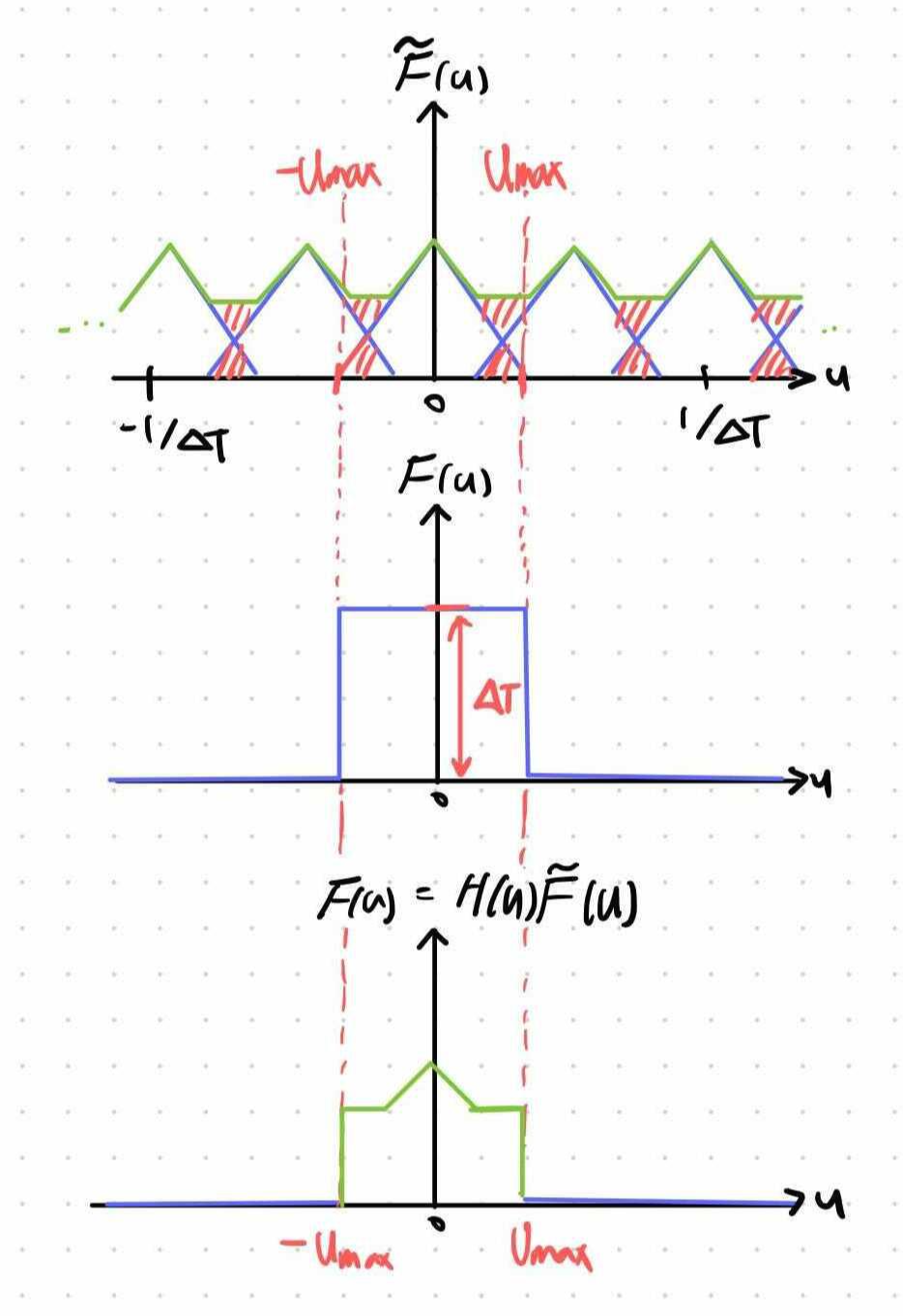
3. Downsampling & Aliasing
그렇다면 본 논문에서 지적한 상황인 downsampling을 할 때는 어떤 일이 발생할까요?
1차원의 신호에 대해서 downsampling을 한다는 것은 다음과 같이 n 축에서 전체적인 경향성을 유지하면서 줄이는 것입니다. 말 그대로 down을 시키는 sampling이니까, 그러다 보니 다음과 같이 aliasing이 발생하는 곳이 생길 수밖에 없게 되고 사실 당연한 일입니다. downsampling을 하게 되면 전체적인 함수를 표현하기 위한 능력을 충분히 가져가면서도 더 적은 sampling rate로 represent 해야 하니 aliasing이 생기는 것입니다.
이를 다시 한번 푸리에 변환을 거친 상태에서 보자면, sampling rate가 감소하는 것이니 그림상으로 주기 함수의 폭이 넓어져 다음과 같이 겹치는 부분이 생겨 aliasing이 생긴다고 생각할 수 있습니다.
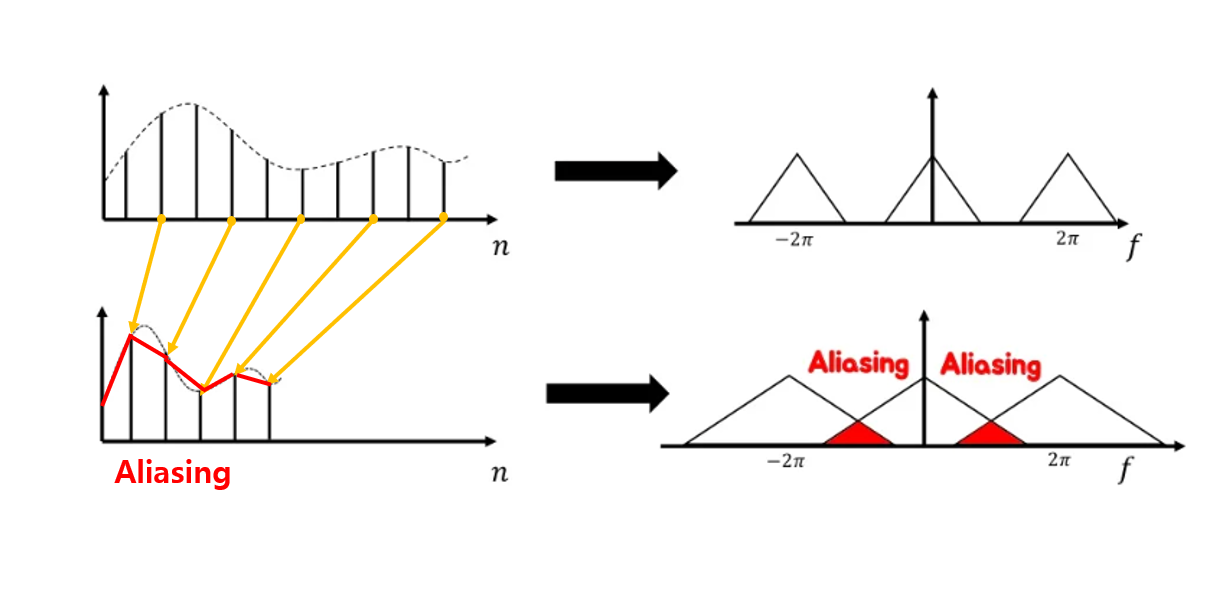
그렇다면 여기서 한 가지 살펴볼 수 있는 점은 downsampling을 하게 되면 다음과 같은 aliasing문제가 발생할 수 있다는 것입니다. 그런데 앞서 이러한 aliasing문제를 해결하기 위해 두 가지 방법을 제시했습니다.
1. sampling rate 늘리기 / 2. anti-aliasing 하지만, 1의 경우에는 downsampling을 하는 과정에서 만족하기 어려운 것이 당연합니다. 따라서 고전적인 신호처리에서는 앞서 살펴봤듯 이러한 문제를 anti-aliasing을 통해 해결합니다. 즉, 이러한 subsampling인 downsampling을 하기에 앞서 blur를 적용한 후에 subsampling을 하는 방법입니다.( 물론 continuous signal을 sampling을 통해 discrete signal로 바꾸는 것은 컴퓨터가 이해해야 하므로 당연히 거쳐야 하는 작업입니다. )
따라서 앞서 살펴봤던 것처럼 low-pass filter를 통해서 anti-aliasing을 하게 될 경우 다음과 같이 subsampling을 거쳤을 때 aliasing이 발생하지 않는 결과를 얻을 수 있습니다.
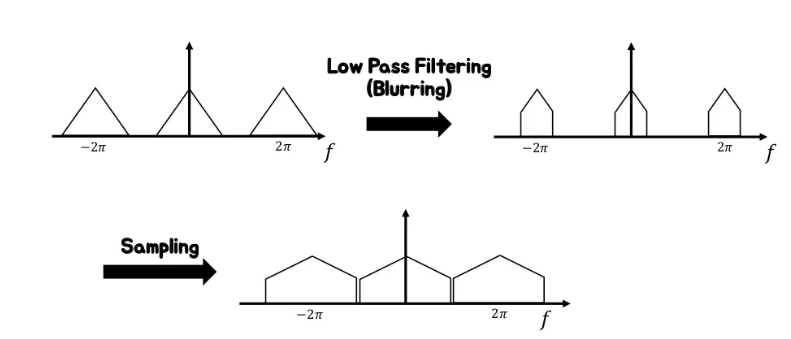
지금껏 살펴봤듯 일반적인 downsampling과정은 신호처리, 이미지 처리, 그래픽스 등에서 주로 subsampling을 하기에 앞서 Prefilter를 거치게 됩니다. 즉, background에서 살펴봤듯 samping 하기 전에 low-pass filter(blurring)를 통과시키는 등의 과정을 거친다는 것입니다. ( 물론 upsampling의 경우 subsampling한 이후에 거치게 됩니다. ) 이렇게 함으로써 anti-aliasing을 하는 것이 성능에 있어 중요한 역할을 했었는데, 딥러닝과 컴퓨터 비전에서는 점차 이러한 anti-aliasing이 잊혀져 왔습니다.
본 논문에서는 놓치고 있던 anti-aliasing에 다시 주목하면서 기존의 컴퓨터 비전과 딥러닝에서 사용하는 기법들의 문제점인 shift variant를 지적하고 이를 해결하기 위해서 anti-aliasing을 어떻게 사용해야 하는지를 주장합니다.
4. CNN - Aliasing
그런데 본 논문에서는 어떤 부분에서 aliasing이 생기고 있길래 이러한 anti-aliasing을 다시 주목할 필요가 있다고 하는 것일까요? 즉 CNN에서 어떤 문제가 aliasing이랑 이어지고 있는 것일까요?
Shift Invariant & Shift Equivariance
이를 위해서는 앞서 언급했던 shift-variance에 대해서 다시 짚고 넘어가야 합니다. 용어들부터 정리하자면 shift invariant는 앞서 abstract에서 대략적으로 얘기했지만 이는 이미지가 shift됐을 때 performance가 바뀌는지입니다. 그렇다면 유사한 말처럼 보이는 shift equivariance는 뭘까요? 이는 shift operation과 feature extraction operation(ex-pooling or convolution) 순서가 commutable하다고 정의됩니다.
일반적으로 대부분의 CNN은 conv layer와 pooling layer 등을 사용합니다. 일반적으로 convolution이나 pooling의 개념 자체는 각각 shift-equivariant하고 shift-invariance하다. 하지만, Deep Neural Network에서 일반적으로 사용하는 conv와 pool은 strided합니다. 이렇게 stride의 개념이 들어가게 되면 CNN에서 conv와 pooling을 통한 downsampling은 앞서 언급했던 Nyquist Sampling Theorem을 무시하게 되고 aliasing을 발생시킵니다.
간단히 살펴보기 위해 strided max pooling을 통해 이러한 문제를 확인해봅시다. 이때 kernel size와 stride는 모두 2입니다. 즉, strided max pooling입니다.
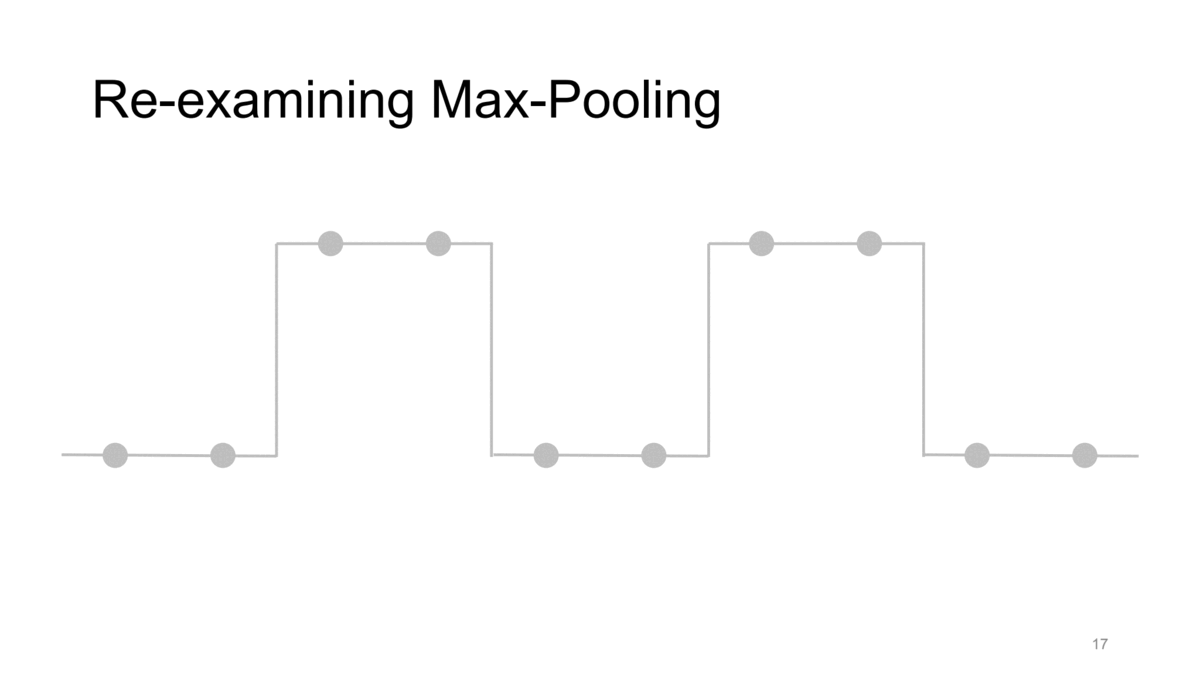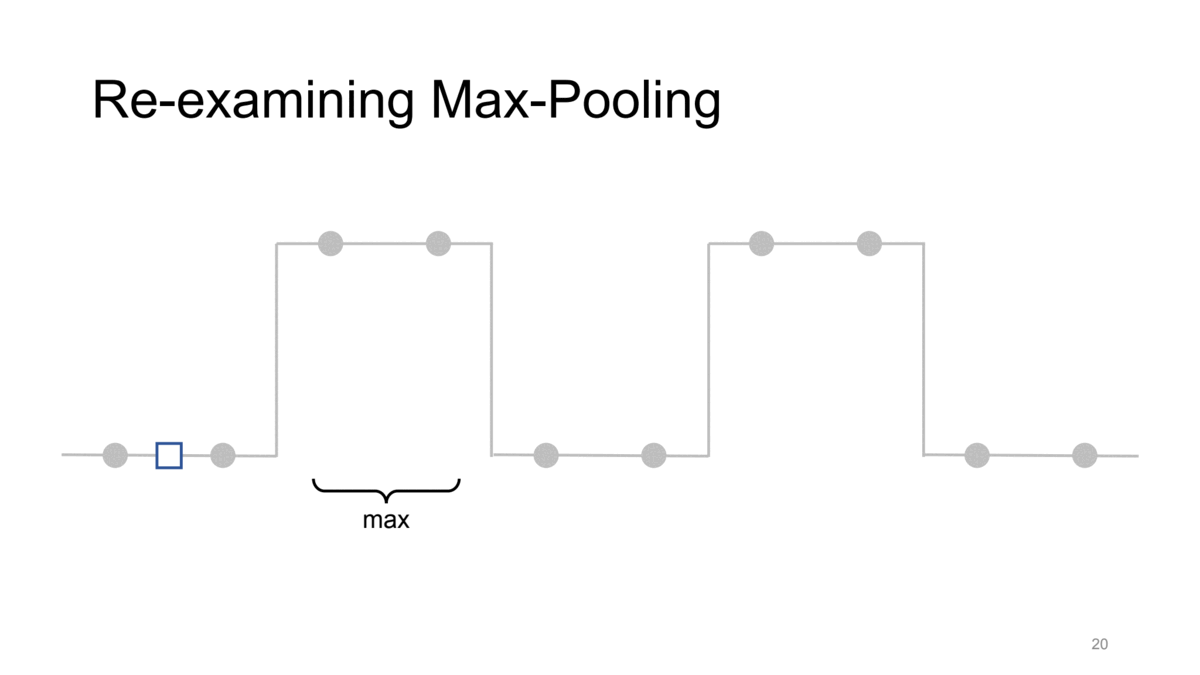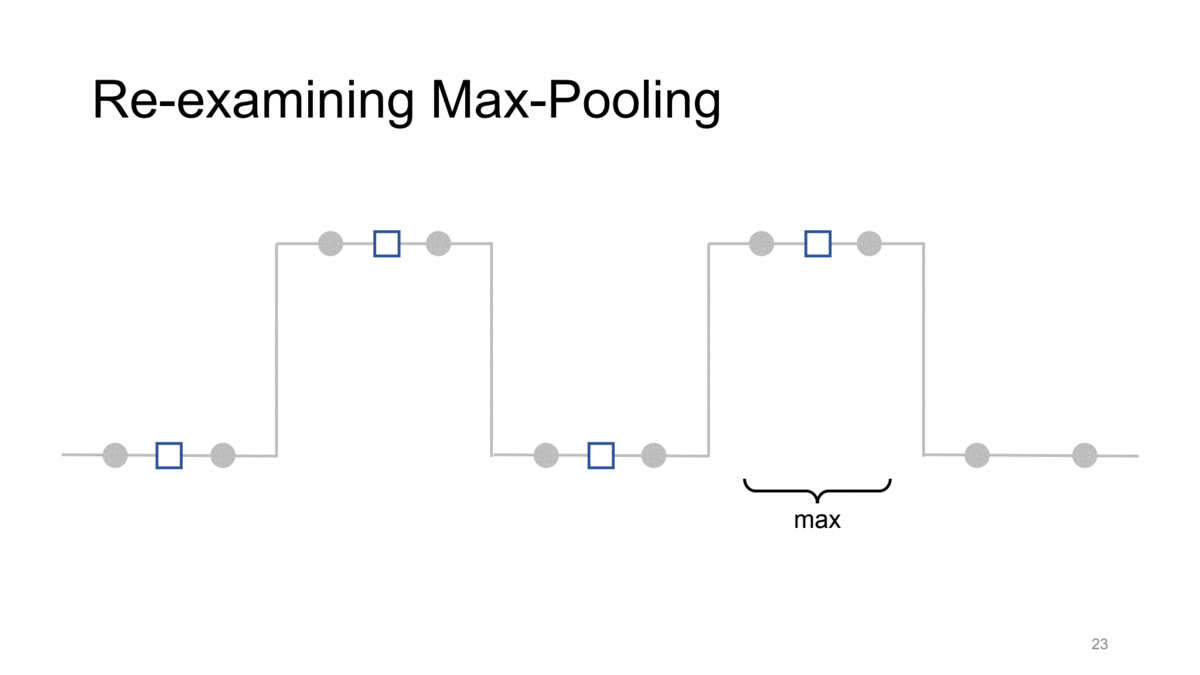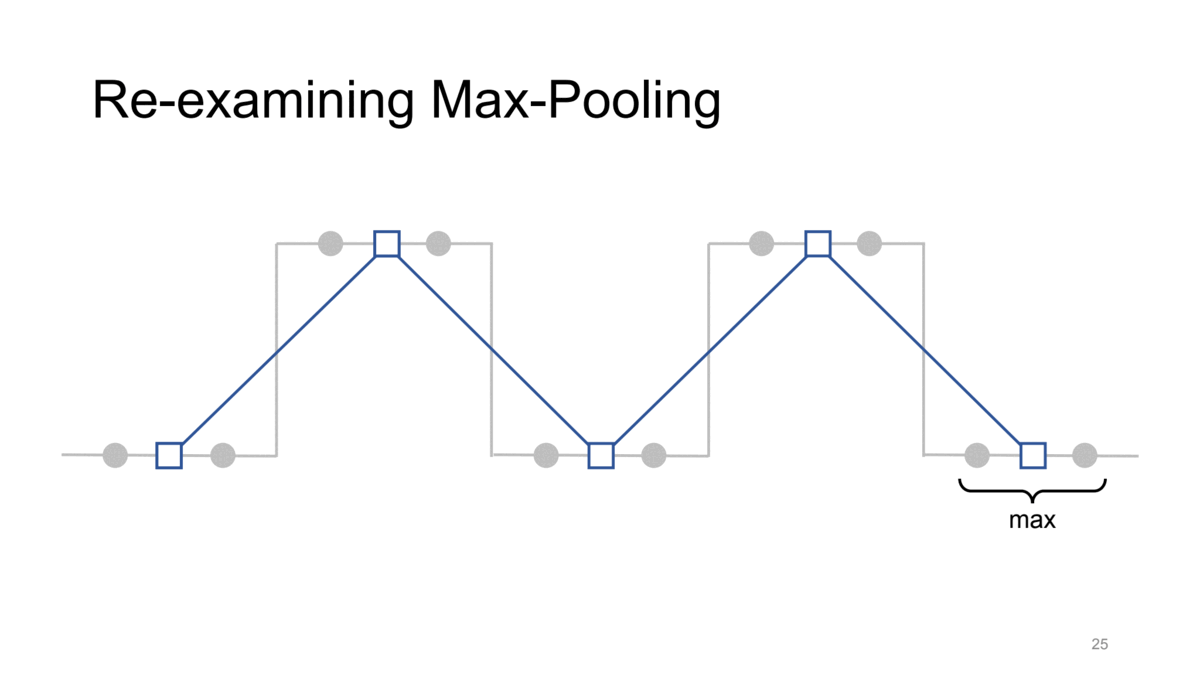
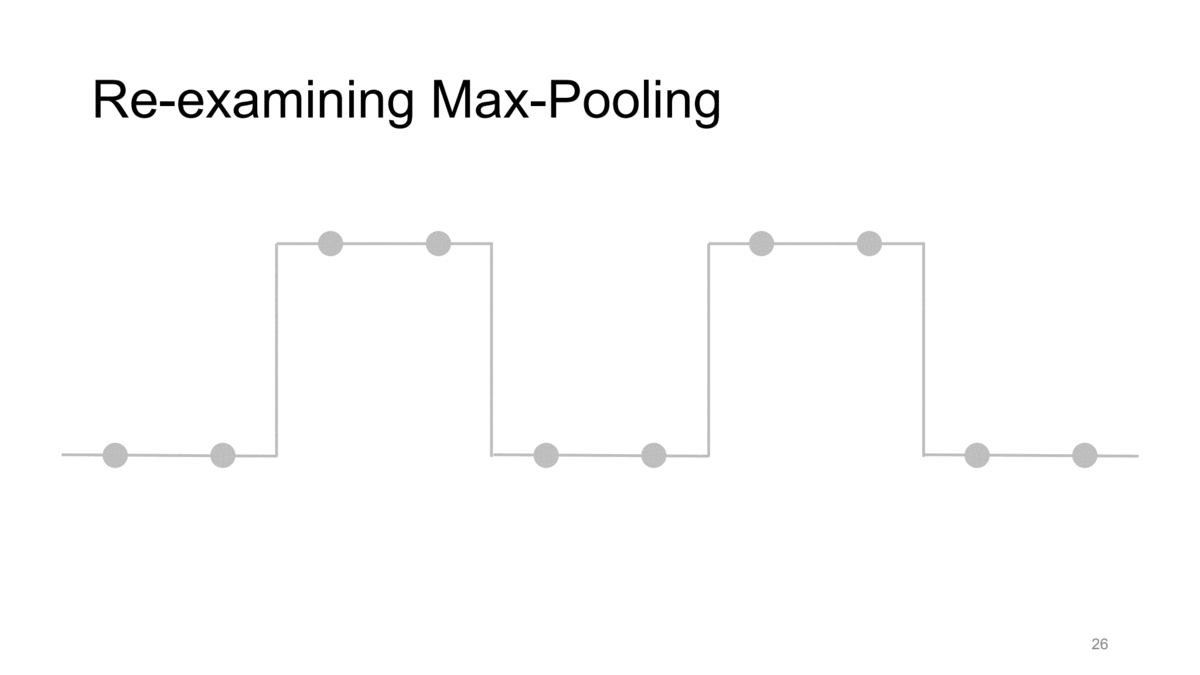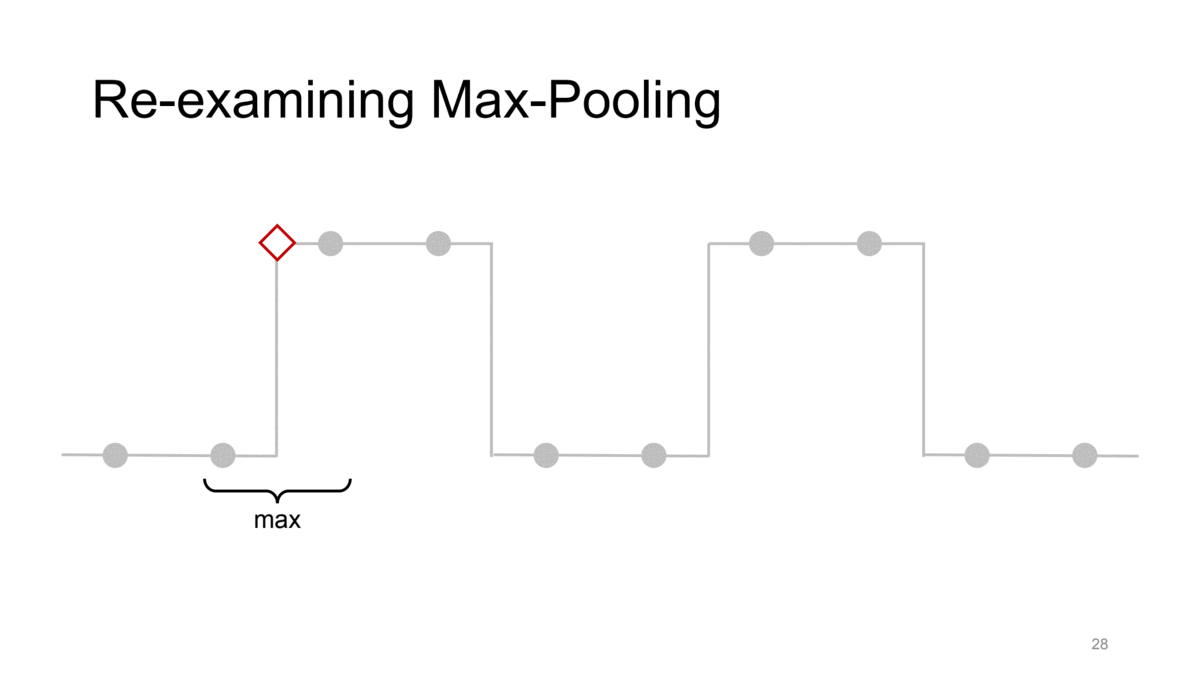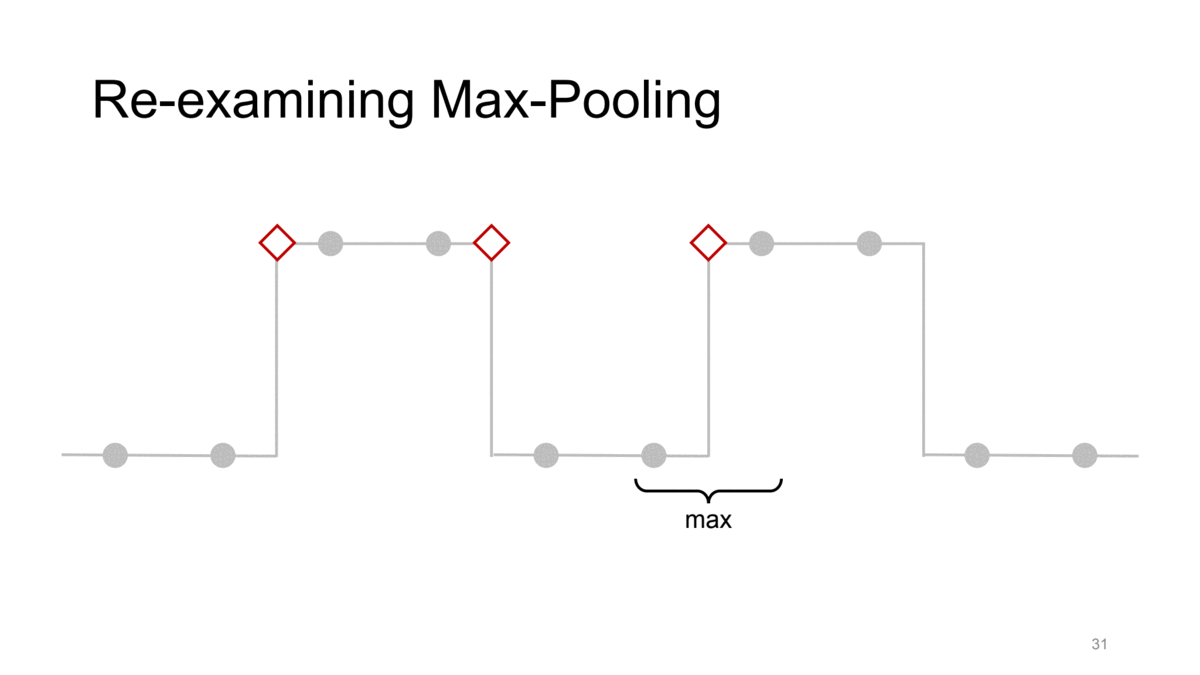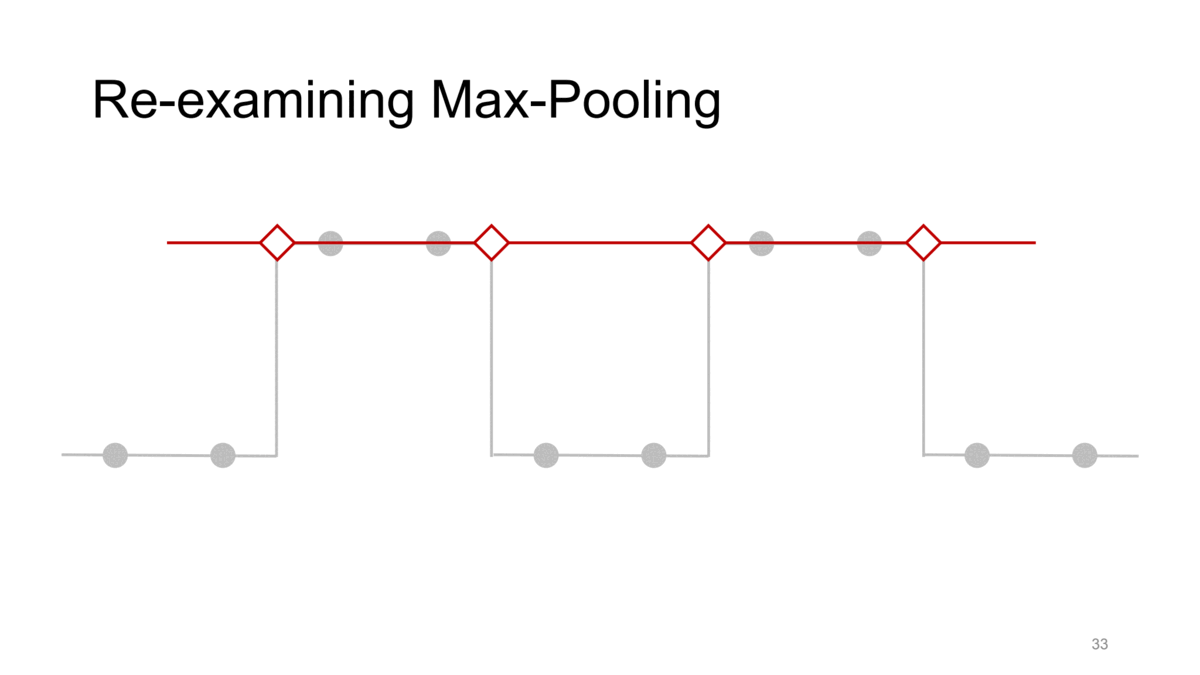
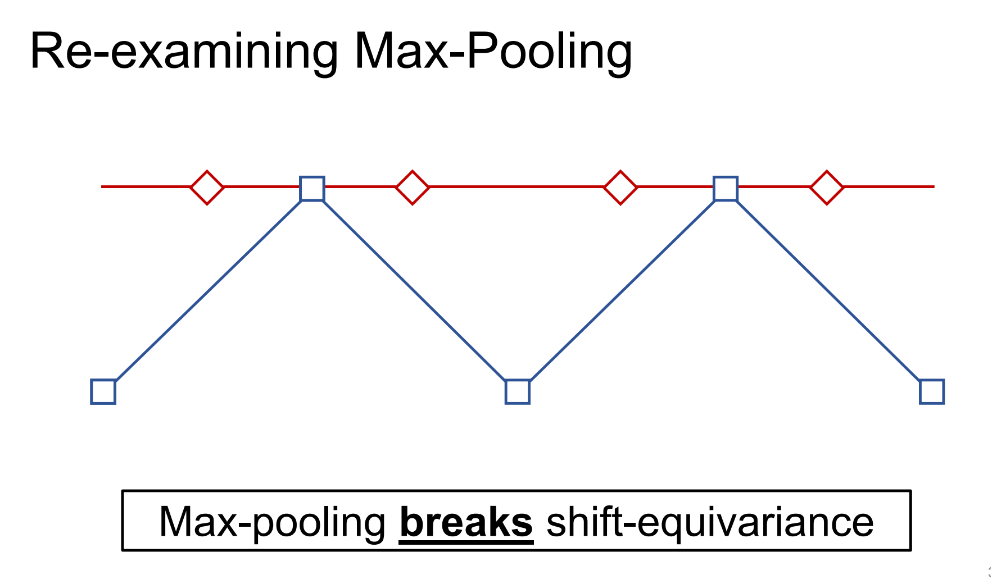
이런 조건에서 각각 max pooling을 수행한다고 생각해봅시다. 그 결과는 위와 같이 좌측 not-shifted signal의 gif에서는 전체적인 신호의 경향성을 어느 정도 유지하는 반면 이를 1칸 shift했을 뿐인데 우측의 gif처럼 같은 max pooling 연산에 대해서 완전히 다른 결과가 나오게 됩니다. 즉, 이러한 CNN의 downsampling method들이 가지는 shift-inequivariance한 특성 때문에 CNN이 shift variant한 결과가 나오게 되는 것입니다.
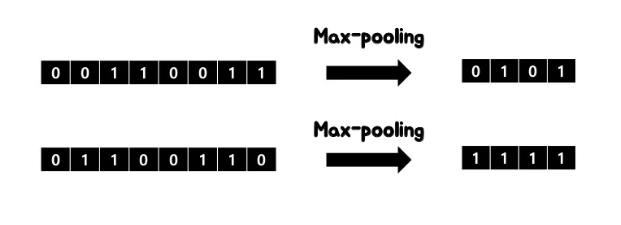
앞서 정의했지만, 다시 짚고 넘어가면 shift equivariance란 shift operation과 feature extraction operation 순서가 commutable한 즉 교환 가능한 것입니다. 위의 예제에서는 max pooling 후에 shift 했을 때의 결과와 max pooling 전에 shift 했을 때의 결과가 완전히 달라지기에 shift-inequivariance하다는 것입니다.
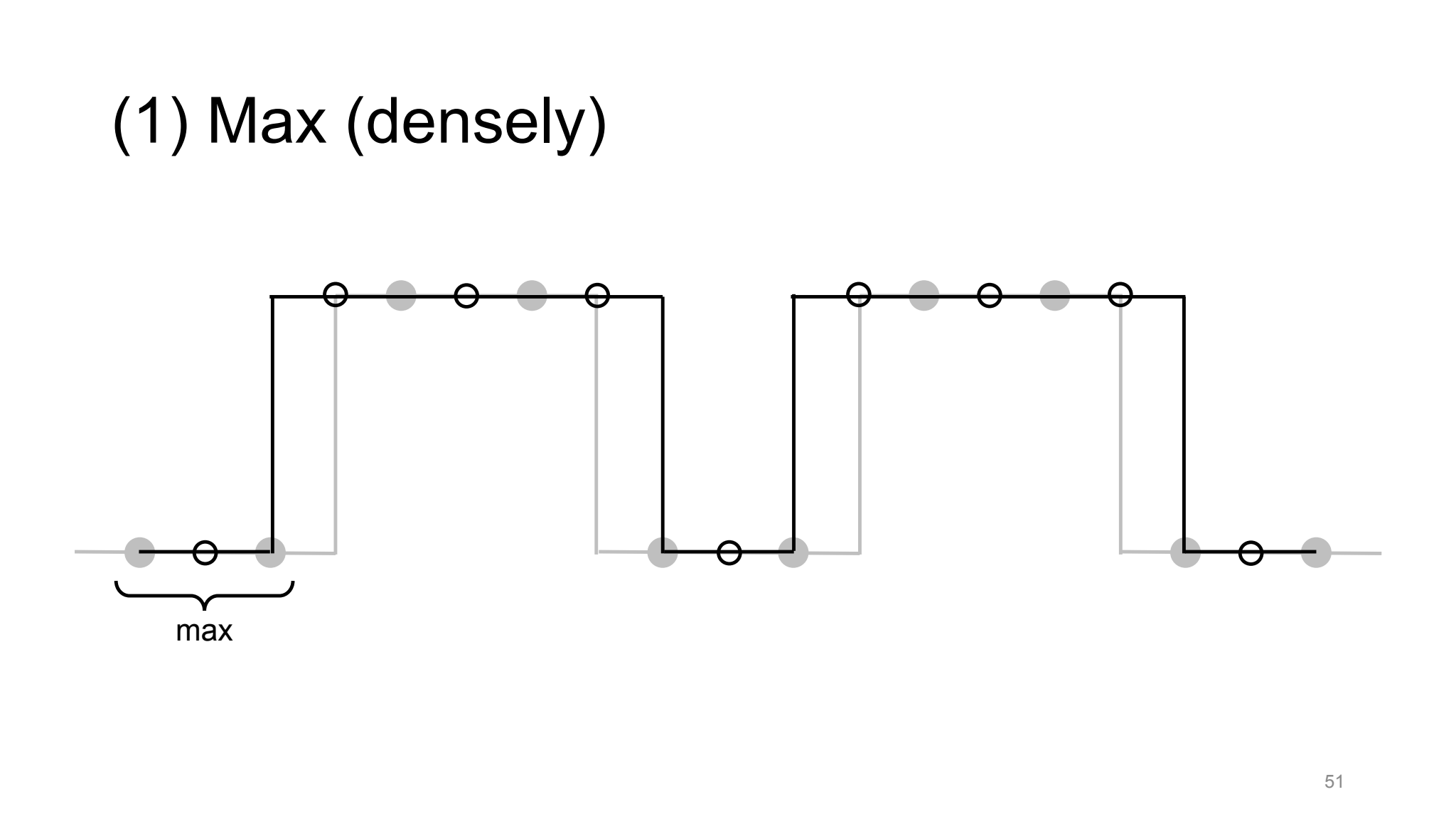
좀 더 자세히 살펴보기 위해서 max pooling을 2가지 operation으로 나눠서 생각해보면. max pooling은 kernel을 움직여가면서 해당 영역에서 max값을 취하는 1. max operation과 취해진 max 값들을 subsampling하는 2.subsampling으로 이루어집니다. 위와 동일한 예시의 max-pooling과정을 방금의 2가지 과정으로 분리해서 생각해봅시다.
Aliasing
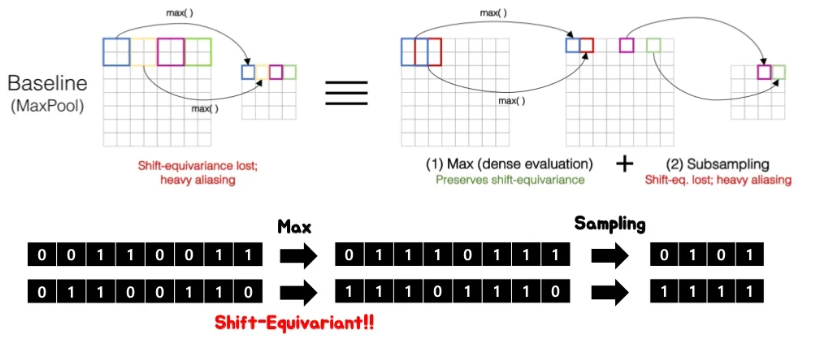
위와 같이 max operation을 거쳤을 때까지만 하더라도 shift-equivariant한 것을 알 수 있습니다. 하지만, subsampling을 하게 되면 shift equivariant하지 못하게 됩니다. 그렇다면 결국 aliasing을 유발하는 operation은 subsampling부분이라는 것입니다.
Anti-Aliasing
이는 앞서 살펴봤듯 일반적인 downsampling과정에서 발생하는 aliasing을 신호처리, 이미지 처리, 그래픽스 등에서 주로 subsampling을 하기에 앞서 Prefilter를 거침으로써 anti-aliasing하는 것을 떠올릴 수 있습니다. 따라서 본 논문에서는 이 두 연산 과정 사이에 filtering을 추가함으로써 anti-aliasing을 달성하게 됩니다.
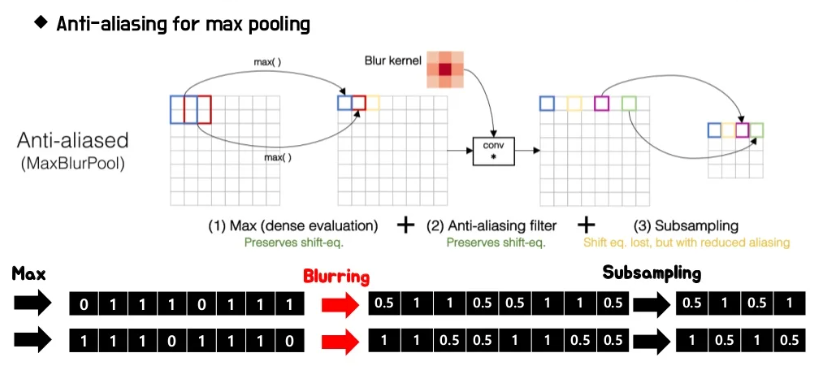
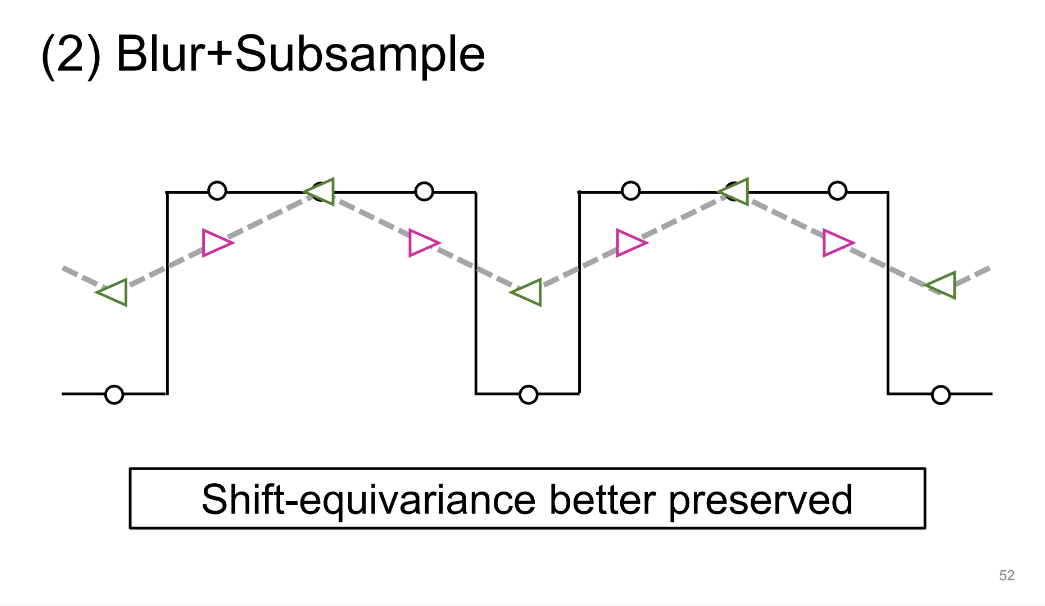
그 결과는 위와 같이 smoothing된 결과를 통해서 shift equivariance한 결과를 얻어내고 이를 통해서 shift invarinat한 CNN을 구성해낼 수 있다는 것입니다.
5. Results
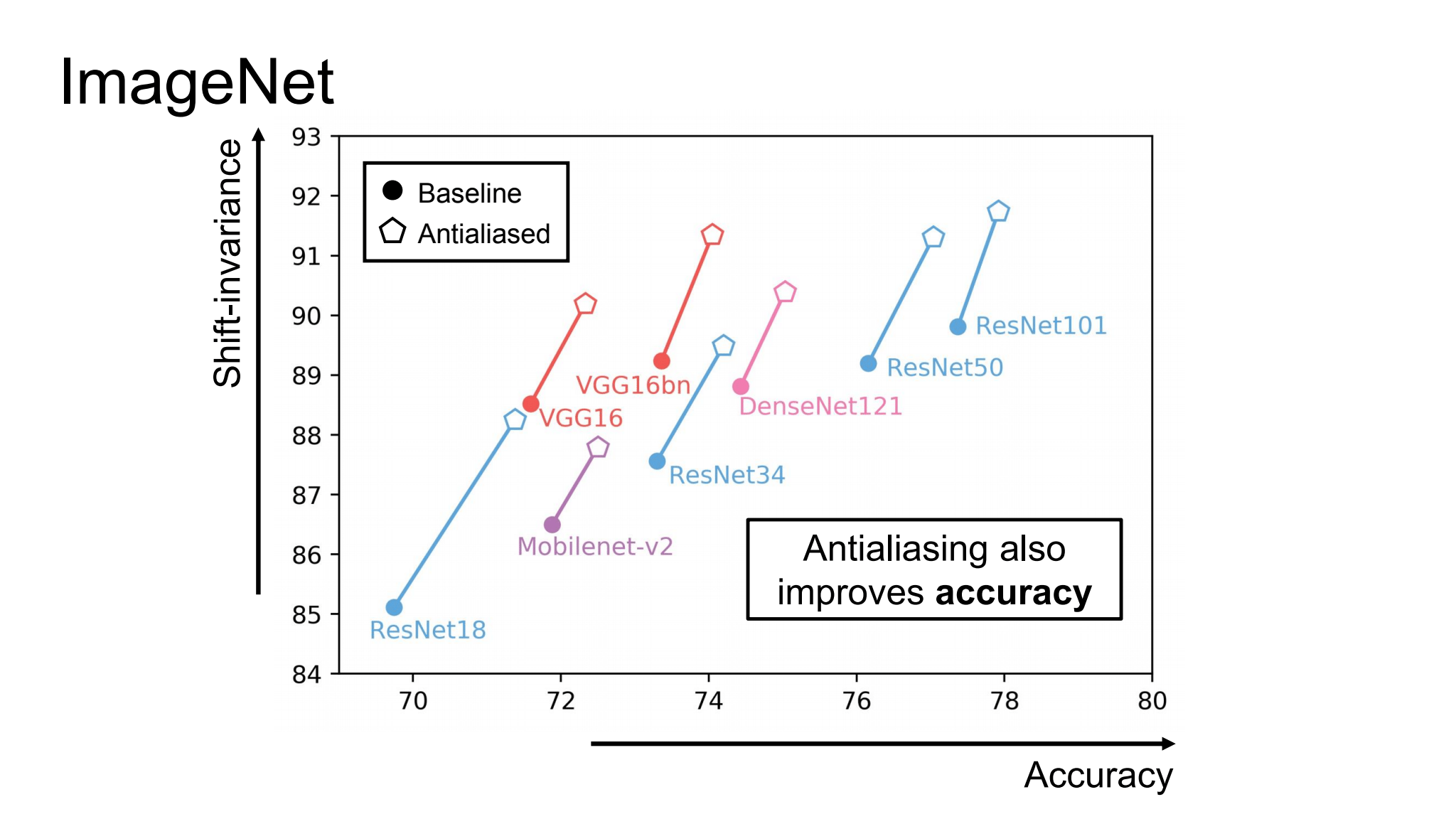
저자들은 이러한 anti-aliasing이 CNN에 근본적인 성능 향상을 가져온다는 것을 실증적으로 증명해냈고 결과는 다음과 같습니다. 특히 전체적으로 훨씬 robust한 결과를 만들어낸다는 점에서 유의미한 연구였다고 생각합니다.

References
https://richzhang.github.io/antialiased-cnns/
https://www.youtube.com/watch?v=oTIBFH6M7YM
https://www.slideshare.net/HyeongminLee3/pr252-making-convolutional-networks-shiftinvariant-again
https://slidesplayer.org/slide/14895988/
https://moonnote.tistory.com/133



